互联网行业从业者在面试的过程中经常会碰到这样一个问题,尤以测试人员和开发人员碰到的几率最高:请说一说你熟悉的几种排序算法。
这个问题或许不是作为唯一考核你专业技能的一个问题,但是如果你能答得上来,面试官肯定会给你打一个比较高的印象分,因为算法直接考察了一个人的**思维和逻辑,分析数据,解决问题的能力。**这也是当下很多高新企业越来越注重和强调的人才素质。
可惜的是很多人在这道题上的表现都很差强人意,要么就是完全答不上来,要么就是听过,但是解释起来却很混乱,这都是源于平时很少了解算法或者对于算法一知半解导致的。
好吧,在介绍冒泡算法之前,肯定还有很多小白连算法的概念都不知道,所以还是先来做一下扫盲吧。**算法(Algorithm)是指解题方案的准确而完整的描述,是一系列解决问题的清晰指令,算法代表着用系统的方法描述解决问题的策略机制。**这个是百度百科的解释,其实说的更简单点,算法就是计算的方法。
回到上面的问题,请列举你熟悉的几种排序算法。
这里小编就给大家介绍常见的几种排序算法:冒泡排序,快速排序,插入排序,选择排序,希尔排序等等,通常,说出两三个你比较熟悉的排序就基本上能搞定面试官了。
咱们这里不会针对每种排序算法去做分析和讲解,咱们来重点谈谈经典排序算法------冒泡排序,说一说它到底是怎么去排的。
首先来了解冒泡这个概念,咱们应该都见过水中的气泡,越往上冒,气泡就越大,所以就用这个生活中常见的现象来描述冒泡排序,把大的数字往上面一直冒,直到所有的数据都是按照从小到大的顺序来排列就是冒泡排序的思想。
假设咱们有几个杂乱无序的数字:4,3,6,2,1,5,那么要通过冒泡排序来将这几个数字按照从小到大的顺序来排序,要怎么做呢?
思路:拿第一个数字跟其他所有数字进行比较,若比它大则交换位置,直到将这些数字中最大的数字冒到最上面,接着再继续第2轮,第3轮,第4轮,第5轮,直到所有大的数组都冒到了上面,这样所有的数据就会按照从小到大来进行排序。
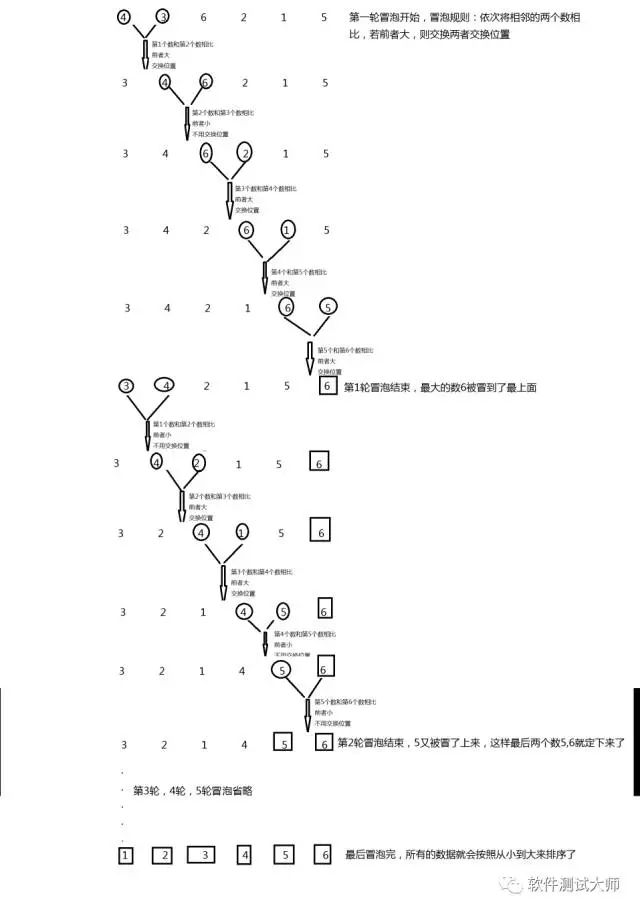
上面是小编画的原理图,如果你还是看不懂,那我们就只能上咱们的终极武器了,下面是小编在网上找到的冒泡懵逼排序图,希望能够帮助你们去理解这个算法的原理。

上面是排序的算法,如果要用代码来实现,该如何写呢?下面小编就用java代码来实现上面这个冒泡排序:

那我们再来分析一下这个算法的复杂度。
我们来看一下整个冒泡过程中数值之间总共比较了多少次。
假设要参与排序的数有n个,则第一轮冒泡第一个数要跟其他n-1个数都进行比较,所以要进行n-1次比较,最大的数被冒到了最上面。
所以第二轮冒泡就相当于前面n-1个数进行冒泡,所以第二轮要进行n-2次比较,以此类推,第三轮比较次数为n-3,最后两个数冒泡的时候只要比较1次。
所以比较次数其实是一个从1到n-1的等差数列的和,所以总共比较次数按照等差数列求和就是:[1+(n-1)](n-1)/2,所以最后得到的次数就是n(n-1)/2次。
这里小编就冒泡排序做了一下简单的介绍,包括冒泡的原理,以及代码实现。至于其他排序算法,感兴趣的同学可以自行百度去了解。
欢迎来到testingpai.com!
注册 关于