白盒笔试题解析
1. 定义
黑盒测试 - 不关注内部结构的测试/基于输入输出的测试
白盒测试 - 基于内部结构的测试
白盒测试的关键: 覆盖度
2. 白盒相关概念
- 语句覆盖 - 设计一套测试 让被测对象中所有语句得到测试覆盖
- 判定覆盖 - 设计一套测试 让被测对象中所有判定得到测试覆盖
- 条件覆盖 - 设计一套测试 让被测对象中所有条件得到测试覆盖
- 路径覆盖 - 设计一套测试 让被测对象中所有路径得到测试覆盖
我们通过一个图来展示什么是“语句”、“判定”、“条件”和“路径“:
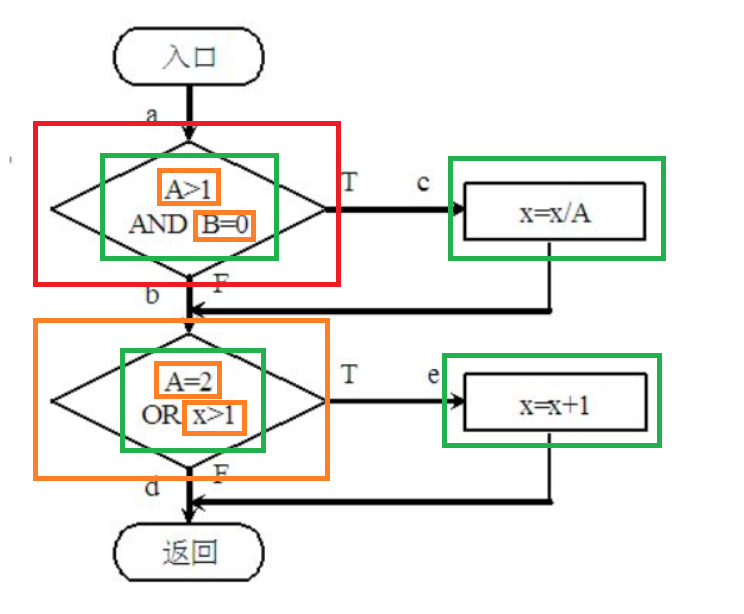
图中,绿色框出部分即为”语句“;红色框出部分即为”判定“;橘色框出部分即为”条件“,所有箭头即为路径。
3. 例题解析
例题1:

解:
- 语句覆盖
我们一步步来,首先来看语句覆盖怎么满足,这段代码中的每一行都是”语句“。
而其中关键所在在于THEN后面这句,他是有可能不执行的。语句覆盖就是要设计出测试数据,使得所有语句都被执行。
那么很简单,只要让两个IF判定判定为”真“即可。
那么我们选择一组数据:
A = 2, B = 0 套进去判断,两个IF判定都取真,THEN语句得到执行,我们就满足了100%语句覆盖。
- 判定覆盖
判定是程序中最常见的一种运算,他的取值为布尔类型,只有两个可能取值:”True“ 和 ”False“(真和假)。
判定可以在程序中创造分支 - 很好理解,就像一条分叉路口,能让程序的执行走向两个不同方向,因此”判定覆盖“又有别名”分支覆盖“。
要满足判定覆盖,就要让所有的判定都取到所有可能取值,即每个判定都取到”真“、”假“各一次。
本题中有两个判定,即”IF“语句,我们就要取一组测试数据,让两个IF都取到真假最少各一次。
那么我们选择一组数据:
A = 2, B = 0; A =0, B = 0 代入这段程序进行判断,发现两个判定的取值为:真真,假假。每个判定都各取到了真假一次,满足了100%语句覆盖。
例题2:

- 语句覆盖
语句覆盖很简单,只要让Then后的语句执行到即可,也就是要让对应的If判定取真。
我们取 X = 2, Y = 1 Z任意,即可满足上述条件,达到100%语句覆盖。
- 分支覆盖
分只覆盖要求所有判定取真假各一次。
我们取 X = 2,Y = 1 Z任意即可让两个判定皆为真。
我们取 X = 0, Y = 0 Z任意即可让两个判定皆为假。
这样我们就满足了题目要求。
例题3:

我们的题目慢慢的难度上升了,第三题就出现了while语句,并且要注意到题中还要求”效力最高“。
要满足判定覆盖,我们先找到题中的判定在哪里。很简单,while语句就是判定,用自然语言解释就是:
当变量i不大于25时,做一件事;当i大于25时,做另一件事。这个判定就是”i大不大于25“.
要满足判定覆盖,很简单,只需要让i小于等于25那么随着while逻辑中i的递增,迟早会超出25,使得判定取到假值。比如我们取 i = 0就可以。
但是题中要求”效率最高“,那是什么意思?
我们注意到,题中的while实现的是一个循环逻辑,我们如果取 i = 0的话,while循环会循环26次。
而如果我们取 i = 25的话,第一次循环,while判定为真,循环内部的逻辑执行1次。执行了1次之后i ++, i的值变为26,while判定为假,循环跳出。
所以取i = 25,循环只执行了一次,判定覆盖即已满足。 i = 25就是可以满足”效力最高“的满足判定覆盖。
例题4:

更难的题来了。
此题还是要满足判定覆盖,我们先把所有判定找出来。此题中的三个if和一个else都是判定。
那么我们就要让所有四个判定分别取到真和假值。
直观的想法,我们取四个值: n = 0 , n = 1, n =2 , n = -1就可以让所有判定都被覆盖到真假所有可能。
但是题中问到,”最少“需要多少个?
我们来看第三个判定后的return语句:
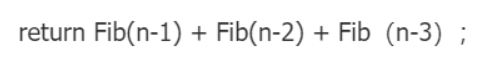
有没有发现什么端倪?这段函数的函数名就叫fib,而函数内部的这段return语句就直接调用了fib函数本身!这就叫**”递归“**。
如果我们代入n = 2这样的数据进入这个函数进行运算,发现return语句演变成以下形式:
return fib(1) + fib(0) + fib(-1)
等于我们又把n = 1, n = 0, n = -1三个取值分别代入了函数中。
也就是说我们只需要 n = 2一组数据,即满足了所有判定的真假覆盖!
4. 练习题
最后留几个练习题我们可以自己尝试解答,欢迎留言写下你的答案:
题1:

题2:

题3:

欢迎来到testingpai.com!
注册 关于