面试必备排序算法 - 选择排序

选择排序(Selection sort)是一种简单直观的排序算法。

算法原理

第一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，然后再从剩余的未排序元素中寻找到最小（大）元素，然后放到已排序的序列的末尾。以此类推，直到全部待排序的数据元素的个数为零。

有无序列表

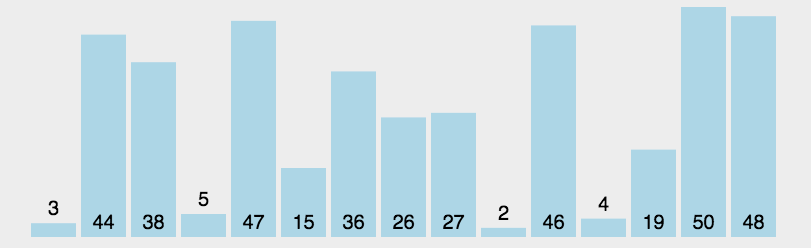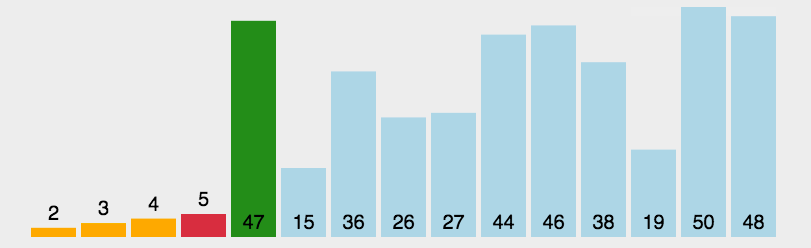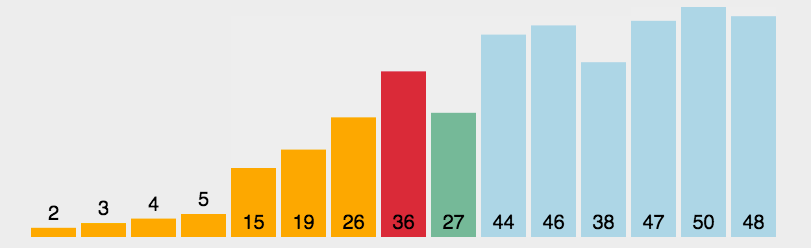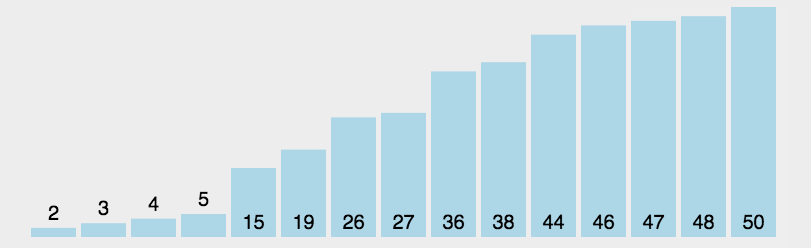
[3,44,38,5,47,115,36,26,27,2,46,4,19,50,48]

进行选择排序，步骤如下：

第一轮从第一个元素开始与下一个元素进行比较，记录较小的元素，再和下下个元素进行比较，记录较小的元素，进行14次比较后找到整个列表中的最小数ls[min]，将它与ls[0]交换位置。
第二轮第二个元素开始与下一个元素进行比较，记录较小的元素，再和下下个元素进行比较，记录较小的元素，进行13次比较后找到从第二个元素开始的列表中的最小数ls[min]，将它与ls[1]交换位置。
第三轮....
第十四轮第十四个元素开始与下一个元素进行比较，找到最后两个元素中的最小数将它与ls[1]交换位置，自此排序完成。

根据上面的步骤归纳总结：

n个元素的列表，需要n-1轮选择排序。每轮选择排序需要的比较次数为n-1-轮次

代码实现

def selection_sort(l):
    n = len(l)
    for i in range(n - 1):  # 进行n-1轮选择排序
        min_index = i  # 预设最小值索引为未排序部分的第一个数
        for j in range(i + 1, n):
            if l[min_index] > l[j]:
                min_index = j
        # 将最小元素放到每次排序的第一个位置
        l[i], l[min_index] = l[min_index], l[i]


ls = [3, 44, 38, 5, 47, 115, 36, 26, 27, 2, 46, 4, 19, 50, 48]

selection_sort(ls)
print(ls)

运行结果：

[2, 3, 4, 5, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50, 115]

分析总结

1. 时间复杂度

在选择排序中，其交换操作介于0（已排序数组）到n-1（逆序数组）之间，时间复杂度为O(n)
比较操作跟数组的初始状态无关，不论待排序数组是有序的还是逆序的，比较操作的次数都是n-1+...+3+2+1=n*(n-1)/2,时间复杂度为O(n2)

2. 空间复杂度

在选择排序算法过程中，临时占用存储空间大小不变，空间复杂度为O(1)

3. 稳定性分析

序列5，8，5，2，9经过一遍选择后，第一个元素5回合2交换，那么原序列中两个5的相对前后顺序就破坏了，所以选择排序是一个不稳定的排序。

4.应用分析

交换操作所需cpu时间比比较所需的cpu时间多，当n值较小时，选择排序的交换操作远小于冒泡排序，此时应当使用选择排序。

测试派 Give testers a home.