测试派 Give testers a home.

登录 注册

面试常问的迭代器和生成器，咱们来剥个 "洋葱"

本贴最后更新于 1263 天前，其中的信息可能已经时移世异

面试常问的迭代器和生成器，咱们来剥个"洋葱"

在第一次接触 Python 的时候，你可能写过类似 for i in [2, 3, 5, 7, 11, 13]: print(i) 这样的语句。for in 语句理解起来很直观形象，比起 C++ 和 java 早期的 for (int i = 0; i < n; i ++) printf("%d\n", a[i]) 这样的语句，不知道简洁清晰到哪里去了。

但是，你想过 Python 在处理 for in 语句的时候，具体发生了什么吗？什么样的对象可以被 for in 来枚举呢？

深入到 Python 的容器类型实现底层，看看迭代器和生成器到底是各方神圣。

可迭代对象和迭代器

在 Python 中一切皆对象，对象的抽象就是类，而对象的集合就是容器。

列表（list: [0, 1, 2]），元组（tuple: (0, 1, 2)），字典（dict: {0:0, 1:1, 2:2}），集合（set: set([0, 1, 2])）都是容器。对于容器，你可以很直观地想象成多个元素在一起的单元；而不同容器的区别，正是在于内部数据结构的实现方法。然后，你就可以针对不同场景，选择不同时间和空间复杂度的容器。

所有的容器都是可迭代的（iterable）。这里的迭代，和枚举不完全一样。迭代可以想象成是你去买苹果，卖家并不告诉你他有多少库存。这样，每次你都需要告诉卖家，你要一个苹果，然后卖家采取行为：要么给你拿一个苹果；要么告诉你，苹果已经卖完了。你并不需要知道，卖家在仓库是怎么摆放苹果的。

严谨地说，迭代器（iterator）提供了一个 next 的方法。调用这个方法后，你要么得到这个容器的下一个对象，要么得到一个 StopIteration 的错误（苹果卖完了）。你不需要像列表一样指定元素的索引，因为字典和集合这样的容器并没有索引一说。比如，字典采用哈希表实现，那么你就只需要知道，next 函数可以不重复不遗漏地一个一个拿到所有元素即可。

而可迭代对象，通过 iter() 函数返回一个迭代器，再通过 next() 函数就可以实现遍历。for in 语句将这个过程隐式化，所以，你只需要知道它大概做了什么就行了。

我们来看下面这段代码，主要向你展示怎么判断一个对象是否可迭代。当然，这还有另一种做法，是 isinstance(obj, Iterable)。


from collections.abc import Iterable

params = [
    1234,
    '1234',
    [1, 2, 3, 4],
    set([1, 2, 3, 4]),
    {1:1, 2:2, 3:3, 4:4},
    (1, 2, 3, 4)
]
  
for param in params:
    print('{} is iterable? {}'.format(param, isinstance(param, Iterable)))
  
# 输出
# 1234 is iterable? False
# 1234 is iterable? True
# [1, 2, 3, 4] is iterable? True
# {1, 2, 3, 4} is iterable? True
# {1: 1, 2: 2, 3: 3, 4mermaid : 4} is iterable? True
# (1, 2, 3, 4) is iterable? True

给出的类型中，除了数字 1234 之外，其它的数据类型都是可迭代的。

生成器

据我所知，很多人对生成器这个概念会比较陌生，因为生成器在很多常用语言中，并没有相对应的模型。

这里，你只需要记着一点：生成器是懒人版本的迭代器

生成器可以想象成是你去买苹果，卖家并没有库存。这样，每次你都需要告诉卖家，你要一个苹果，然后卖家采取行为，立马生成 1 个苹果（生成速度极快）：要么给你拿一个苹果；要么告诉你，苹果已经卖完了。

对比看一下以下代码

import os
import psutil
import time
import functools

def log_execution_time(func):
    @functools.wraps(func)
    def wrapper(*args, **kwargs):
        start = time.perf_counter()
        res = func(*args, **kwargs)
        end = time.perf_counter()
        print('{} took {} ms'.format(func.__name__, (end - start) * 1000))
        return res
    return wrapper
  

# 显示当前 python 程序占用的内存大小
def show_memory_info(hint):
    pid = os.getpid()
    p = psutil.Process(pid)
  
    info = p.memory_full_info()
    memory = info.uss / 1024. / 1024
    print('{} memory used: {} MB'.format(hint, memory))

@log_execution_time
def test_iterator():
    show_memory_info('initing iterator')
    list_1 = [i for i in range(100000000)]
    show_memory_info('after iterator initiated')
    print(sum(list_1))
    show_memory_info('after sum called')
  
@log_execution_time
def test_generator():
    show_memory_info('initing generator')
    list_2 = (i for i in range(100000000))
    show_memory_info('after generator initiated')
    print(sum(list_2))
    show_memory_info('after sum called')

test_iterator()
print()
test_generator()

########## 输出 ##########
# initing iterator memory used: 10.16796875 MB
# after iterator initiated memory used: 3664.34765625 MB
# 4999999950000000
# after sum called memory used: 3664.34765625 MB
# test_iterator took 6179.794754018076 ms

# initing generator memory used: 19.140625 MB
# after generator initiated memory used: 19.14453125 MB
# 4999999950000000
# after sum called memory usedmermaid : 19.171875 MB
# test_generator took 4912.561981996987 ms

迭代器是一个有限集合，生成器则可以成为一个无限集。

一个迭代器很简单，[i for i in range(100000000)]就可以生成一个包含一亿元素的列表。每个元素在生成后都会保存到内存中，你通过代码可以看到，它们占用了巨量的内存，内存不够的话就会出现 OOM 错误。

我们并不需要在内存中同时保存这么多东西，比如对元素求和，我们只需要知道每个元素在相加的那一刻是多少就行了，用完就可以扔掉了。

于是，生成器的概念应运而生，在你调用 next() 函数的时候，才会生成下一个变量。生成器在 Python 的写法是用小括号括起来，(i for i in range(100000000))，即初始化了一个生成器。

这样一来，你可以清晰地看到，生成器并不会像迭代器一样占用大量内存，只有在被使用的时候才会调用。而且生成器在初始化的时候，并不需要运行一次生成操作，相比于 test_iterator()，test_generator()函数节省了一次生成一亿个元素的过程，因此耗时明显比迭代器短。

用生成器来观测一波数学公式

示例，数学中有一个恒等式，(1 + 2 + 3 + ... + n)^2 = 1^3 + 2^3 + 3^3 + ... + n^3 的证明

def generator(k):
    i = 1
    while True:
        yield i ** k
        i += 1

gen_1 = generator(1)
gen_3 = generator(3)
print(gen_1)
print(gen_3)

def get_sum(n):
    sum_1, sum_3 = 0, 0
    for i in range(n):
        next_1 = next(gen_1)
        next_3 = next(gen_3)
        print('next_1 = {}, next_3 = {}'.format(next_1, next_3))
        sum_1 += next_1
        sum_3 += next_3
    print(sum_1 * sum_1, sum_3)

get_sum(8)

########## 输出 ##########
# <generator object generator at 0x10c30d3d0>
# <generator object generator at 0x10c6d61d0>
# next_1 = 1, next_3 = 1
# next_1 = 2, next_3 = 8
# next_1 = 3, next_3 = 27
# next_1 = 4, next_3 = 64
# next_1 = 5, next_3 = 125
# next_1 = 6, next_3 = 216
# next_1 = 7, next_3 = 343
# next_1 = 8, next_3 = 512
# 1296 1296

这段代码中，你首先注意一下 generator() 这个函数，它返回了一个生成器。

接下来的 yield 是魔术的关键。对于初学者来说，你可以理解为，函数运行到这一行的时候，程序会从这里暂停，然后跳出，不过跳到哪里呢？答案是 next() 函数。那么 i ** k 是干什么的呢？它其实成了 next() 函数的返回值。

这样，每次 next(gen) 函数被调用的时候，暂停的程序就又复活了，从 yield 这里向下继续执行；同时注意，局部变量 i 并没有被清除掉，而是会继续累加。我们可以看到 next_1 从 1 变到 8，next_3 从 1 变到 512。

聪明的你应该注意到了，这个生成器居然可以一直进行下去！没错，事实上，迭代器是一个有限集合，生成器则可以成为一个无限集。我只管调用 next()，生成器根据运算会自动生成新的元素，然后返回给你，非常便捷。

来碰碰“力扣”的生成器题目-判断子序列

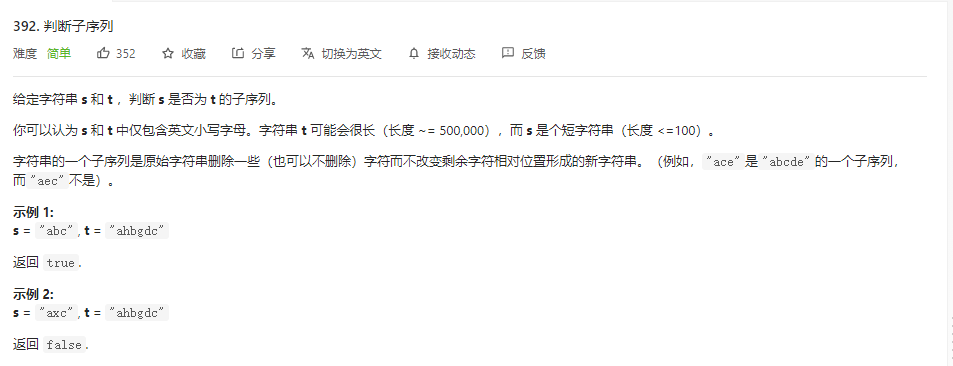
image.png

先来解读一下这个问题本身。序列就是列表，子序列则指的是，一个列表的元素在第二个列表中都按顺序出现，但是并不必挨在一起。举个例子，[1, 3, 5] 是 [1, 2, 3, 4, 5] 的子序列，[1, 4, 3] 则不是。

要解决这个问题，常规算法是贪心算法。我们维护两个指针指向两个列表的最开始，然后对第二个序列一路扫过去，如果某个数字和第一个指针指的一样，那么就把第一个指针前进一步。第一个指针移出第一个序列最后一个元素的时候，返回 True，否则返回 False。

不过，这个算法普通写的话，写下来怎么也得十行左右。

那么如果我们用迭代器和生成器呢？

def is_subsequence(ls, sub):
    ls = iter(ls)
    return all(i in ls for i in sub)

print(is_subsequence([1, 2, 3, 4, 5],[1, 3, 5]))
print(is_subsequence([1, 2, 3, 4, 5],[1, 4, 3]))

########## 输出 ##########

# True
# False

哦吼，这简短的几行代码就搞定了。

如果看不懂的话，咱们再来拆分一下

def is_subsequence(a, b):
    b = iter(b)
    print(b)
 
    gen = (i for i in a)
    print(gen)
 
    for i in gen:
        print(i)
 
    gen = ((i in b) for i in a)
    print(gen)
 
    for i in gen:
        print(i)
 
    return all(((i in b) for i in a))
 
print(is_subsequence([1, 3, 5], [1, 2, 3, 4, 5]))
print(is_subsequence([1, 4, 3], [1, 2, 3, 4, 5]))
 
########## 输出 ##########
 
<list_iterator object at 0x000001E7063D0E80>
<generator object is_subsequence.<locals>.<genexpr> at 0x000001E70651C570>
1
3
5
<generator object is_subsequence.<locals>.<genexpr> at 0x000001E70651C5E8>
True
True
True
False
<list_iterator object at 0x000001E7063D0D30>
<generator object is_subsequence.<locals>.<genexpr> at 0x000001E70651C5E8>
1
4
3
<generator object is_subsequence.<locals>.<genexpr> at 0x000001E70651C570>
True
True
False
False

首先，第二行的b = iter(b)，把列表 b 转化成了一个迭代器，这里我先不解释为什么要这么做。

接下来的gen = (i for i in a)语句很好理解，产生一个生成器，这个生成器可以遍历对象 a，因此能够输出 1, 3, 5。而 (i in b)需要好好揣摩，这里你是不是能联想到 for in 语句？

没错，这里的(i in b)，大致等价于下面这段代码：

while True:
    val = next(b)
    if val == i:
        yield True

这里非常巧妙地利用生成器的特性，next() 函数运行的时候，保存了当前的指针。比如再看下面这个示例：

b = (i for i in range(5))
 
print(2 in b)
print(4 in b)
print(3 in b)
 
########## 输出 ##########
 
True
True
False

至于最后的 all() 函数，就很简单了。它用来判断一个迭代器的元素是否全部为 True，如果是则返回 True，否则就返回 False.

于是到此，我们就很优雅地解决了这道面试题。不过你一定注意，面试的时候尽量不要用这种技巧，因为你的面试官有可能并不知道生成器的用法。（玩笑话，毕竟不是人人都跟你一样强）

总结

4 操作
FlawlessK 在 2020-11-12 16:47:43 开启了该帖的回帖
FlawlessK 在 2020-11-12 16:39:50 关闭了该帖的回帖
FlawlessK 在 2020-11-12 10:38:23 更新了该帖
FlawlessK 在 2020-11-12 10:36:41 更新了该帖
长沙 位置
1 收藏
4 操作
2279 88 498 617 53 70 34 919

相关帖子

随便看看

回帖
请输入回帖内容 ...