希尔排序按其设计者希尔(Donald Shell)的名字命名,该算法由希尔 1959 年公布。希尔排序(Shell's Sort)是插入排序的一种又称"缩小增量排序",是直接插入排序算法的一种高效的改进版本。
希尔排序是基于插入排序的以下两点性质而提出改进方案的:
- 插入排序在对几乎已经排好序的数据操作时,效率高,可以达到线性排序的效率。
- 但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位
算法原理
算法先将要排序的一组数字按某个增量d分成若干个组,每组中记录的下标相差d。对所有的组进行排序,然后再用一个较小的增量对它进行分组,在每组中再进行排序。直到增量减少到1时,整个排序的数被分成一组,排序完成。
一般初次取序列的一半为增量,以后每次减半,直到增量为1.
给定实例的希尔排序过程如下:
假设待排序列表有10个记录,分别是:
[49, 38, 65, 97, 76, 13, 27, 49, 55, 04]
增量序列的取值依次为:
5,2,1
排序过程图如下:

代码实现
def shell_sort(ls):
"""
希尔排序
:param ls:
:return:
"""
n = len(ls) # 数组长度
d = n // 2 # 初始增量为数组长度的一半
while d > 0:
# 插入排序
for i in range(d, n):
cur_index = i # 当前索引
pre_index = i - d # 前一个待比较索引
while pre_index >= 0:
if ls[cur_index] < ls[pre_index]: # 如果当前元素小于前一个元素
# 交换
ls[cur_index], ls[pre_index] = ls[pre_index], ls[cur_index]
# 更换当前索引
cur_index = pre_index
# 计算下一个待比较的索引
pre_index -= d
else:
break
# 增量除以2
d = d//2
分析总结
1. 时间复杂度
本质上讲,希尔排序算法是直接插入排序算法的一种改进,减少了其复制的次数,速度要快很多。 原因是,当n值很大时数据项每一趟排序需要移动的个数很少,但数据项的距离很长。当n值减小时每一趟需要移动的数据增多,此时已经接近于它们排序后的最终位置。 正是这两种情况的结合才使希尔排序效率比插入排序高很多。希尔排序的时间的时间复杂度为O(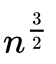 ),希尔排序时间复杂度的下界是n*log2n。
),希尔排序时间复杂度的下界是n*log2n。
2. 空间复杂度
在希尔排序算法过程中,临时占用存储空间大小不变,空复杂度为O(1)
3. 稳定性分析
由于多次插入排序,我们知道一次插入排序是稳定的,不会改变相同元素的相对顺序,但在不同的插入过程中,相同元素可能在各自的插入排序中移动,最后其稳定性就会被打乱,所以希尔排序是不稳定的。
4.应用分析
希尔排序没有快速排序算法快 O(n(logn)),因此中等大小规模表现良好,对规模非常大的数据排序不是最优选择。但是比O(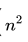 )复杂度的算法快得多。并且希尔排序非常容易实现,算法代码短而简单。 此外,希尔算法在最坏的情况下和平均情况下执行效率相差不是很多,与此同时快速排序在最坏的情况下执行的效率会非常差。专家们提倡,几乎任何排序工作在开始时都可以用希尔排序,若在实际使用中证明它不够快,再改成快速排序这样更高级的排序算法.
)复杂度的算法快得多。并且希尔排序非常容易实现,算法代码短而简单。 此外,希尔算法在最坏的情况下和平均情况下执行效率相差不是很多,与此同时快速排序在最坏的情况下执行的效率会非常差。专家们提倡,几乎任何排序工作在开始时都可以用希尔排序,若在实际使用中证明它不够快,再改成快速排序这样更高级的排序算法.
欢迎来到testingpai.com!
注册 关于